Blog

Data-oriented design

Asbjørn Faurholt Software Developer, Solita

Published 04 Aug 2023

Reading time 11 min

Data-oriented design is a programming paradigm focused on the efficient transformation of data, focusing on high performance, and minimising complexity and side-effects. This article is targeted towards readers that have at least a fundamental understanding of computer science and how computer hardware functions. Topics such as memory management, CPU cache and object-oriented programming will be discussed. As a caveat to any talk about performance, it is important to measure before and after, to see the real impact on given hardware. It is difficult to determine if a given system would benefit from a given performance technique, without actually implementing it.

What is data-oriented design?

As stated above, data-oriented design (DOD) is a programming paradigm like object-oriented programming (OOP), functional programming (FP) or procedural programming.

It is often easier to explain DOD by contrasting it to other paradigms.

To use OOP as an example, OOP concerns itself with objects (which are instantiations of classes), which contain fields or “attributes”, which is our data, and procedures called “methods”, which is our code.

The OOP paradigm invites the programmer to model the problem domain directly in the code, such as making a “car” object, with “wheels”, “colour” and “brand” attributes, and a “drive” method.

This is a convenient way to design the system, as it is rather intuitive. Unfortunately, the resulting system is often not what the problem domain actually looks like, or rather, a solution for a given problem domain is not a 1-to-1 translation of the real world into code.

The high level of abstraction in OOP also creates a clear separation from the underlying computer hardware. The abstract objects can vary greatly in structure making it harder to search for them and store them under the same conditions in memory. An OOP system would ask the hardware to treat a “dog” object and a “car” object similarly in memory.

DOD eliminates a lot of the hardware abstractions. It accepts that the role of a system is to take input data, transform it on given hardware, and give output data.

Data, in this sense, could just be an array of numbers, such as [3, 4, 5], which doesn’t mean much on its own, but if it was put in the context of coordinates in the x, y and z axis, it suddenly gains meaning. So, the DOD programmer accepts that data can be similar, such as the number of legs on a dog, for instance, 4, or the number of wheels on a car, for instance, 4, again. It is only in the context of dog legs or car wheels that the number 4 has a specific meaning.

This approach is particularly helpful for real-time graphical applications, such as in video games, since the position of one object isn’t fundamentally different from the position of another object. Likewise, the two positions will have the same data transformations applied to them, such as translating them. With this knowledge, positions can be stored together, creating packed memory which the hardware prefers, and performing the same transformation to all of it, something that the computer also likes.

Thus, we begin to see that data isn’t the problem domain, as it is fundamentally meaningless. In the same vein, the problem domain is also not the code. The “dog” as such, doesn’t exist as an object. In this way, the programmer gives up some of the human-friendly readability, but in return, they also gain freedom from the constraints abstractions like this would bring, and its effects on the underlying hardware. To DOD there is no difference between a car driving or a dog moving if all it’s doing is changing its position. In this regard, we’re also closer to the much sought-after code reuse, as there are very few algorithms that cannot be reused on primitive types.

We have also come to another truth for the DOD programmer, which is that our data, without meaning, has no structure. There is no “dog” structure. The dog is rather implicit from a combination of data within the system. And in many regards, it is easier for the DOD programmer to have evolving systems, since they don’t have to update a dog object, and all the objects dependent on the dog object, such as a kennel or dog owner. Rather, they just add more data to the system and more transformations.

In fact, it could be said, DOD doesn’t require a final design of the system as it isn’t context-dependent, rather it only concerns itself with the data and transformations needed to meet use cases. On the other hand, this lack of strict structure and expectation that the programmer understands the intricacies of the underlying hardware requires more discipline of the programmer since the programming paradigm doesn’t hold his/her hands.

Why use data-oriented design?

Less complexity

To quantify the complexity of a given system we often use cyclomatic complexity. This is a metric that concerns itself with the branching of flow control. We start at one and increase the value by one for each if statement, while statement and each case of a switch statement.

Virtual calls, such as when using inheritance, for instance, an interface, essentially work like a switch statement by looking into a call table and picking the correct function pointer. We therefore also count each override.

However, this is typically not what causes the most complexity for a system – that is caused by “state”. Consider a light switch. It can be turned on or off. It has two states. Now consider two light switches. Each permutation is a state; off/off, on/off, off/on and on/on. If we then wanted to track whether the room was “very bright” (on/on), one might be tempted to have this as a boolean.

With this in mind, it is important to eliminate unnecessary flow control branching, such as those that only exist due to using a specific programming paradigm, and not to solve the use-case.

Likewise, we should avoid introducing an extra state to our system, that could instead be implicitly determined. For instance, if we characterise having both light switches on, as being “very bright”. We can introduce a boolean that reflects if it is very bright, but this is an extra state, that isn’t strictly needed. Instead, we should interrogate the state of our current system to see if “very bright” is met – whether both light switches are set to “on”.

Better performance

Something important to note about flow control branching and state is its statistical nature. What is the most common use case? Not necessarily the domain use case, but the actual use case in the system under use. By considering which parts of our system are the most common, we can program for these cases, and help the branch predictor. If we take our light switch from earlier and assume it has a random chance of being either on or off, we will get a branch prediction success rate of 50 %. This means that 50 % of the time, the CPU guesses wrong and must retrieve different instructions into the cache, losing up to 10 to 20 cycles each time. While 10 to 20 cycles don’t seem like a big deal, remember this is simply for a two-state system with a single branch. If we’re working with real-time datasets of considerable size, this will quickly add up. Even if performance isn’t an explicit feature of a project, it still makes sense to improve it by embracing a methodology that defaults to making optimal performance choices.

A way to solve our light switch use case would be to have two different lists. One containing all light switches that are on and one containing all light switches that are off. If we need to perform a given transform only on light switches that are on, we simply give it the list of light switches that are on. Compared to having a single list with all light switches, we now have no need to check their state within our procedure, thus avoiding branching and potential branch prediction misses, since we now know that all light switches we operate on are turned on.

In this example, turning a light switch off would simply be deleting it from the “on”-list and inserting it into the “off”-list.

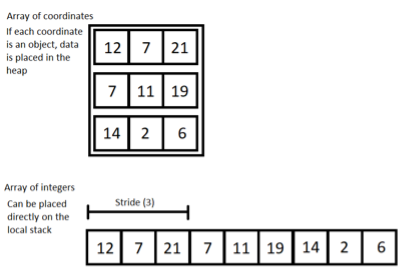
We also help the computer by only working with primitive types. We work with “structs of arrays” rather than “arrays of structs”. An example could be an array of positions in 3D space. The positions might be a vector object, or it might be a 3-dimensional array. However, the interpretation that the numbers in this array are actually positions, doesn’t have to be part of the system. Instead, we can simply store every number in a single one-dimensional array of integers, placing the 3 coordinates for a given position sequentially after each other. Now, to get the 3 coordinates for a particular position, we take the positions index multiplied by the stride, which in this case would be three. The 3 numbers at the resulting index and the next two elements are then the coordinates for the position (see Figure 1).

Figure 1. Storing coordinates

Now we have a much more performant array, which can operate without object lifetime eating into our performance budget since we’re simply using primitive numbers. It is also worth noting that most languages store objects on the heap, which would mean when the CPU seeks through our array and finds the position, it would then have to seek again to dereference, and only then would it find the actual data we require. By tightly packing our data as primitives of the same byte size and same type with the same stride, making sure it fits in the cache, we ensure much better seek times. See Figure 2 for an illustration of the speed difference between different parts of the storage hierarchy.

Figure 2. Storage hierarchy

Handling changing requirements

While OOP lends itself very well to fast implementation, it is quite poor when the data schema changes.

It is often the case that when maintaining OOP-systems, classes grow over time, as requirements for the data schema change. We would actually prefer that only the parts where the data is transformed – the procedures – were modified. This is why DOD uses controllers that consume primitive types, have no side effects, and output primitive types.

In a given system it is common for the data schema to change over time, such as adding a colour to a light switch, instead of it simply being on or off. With DOD, instead of growing our light switch class, we simply add the new data to the system as primitives, without having to refactor other dependencies the light switch object might have had in an OOP system.

How to implement data-oriented design

One way to decouple data from its meaning is to apply database normalisation techniques. In many ways, if we were to consider our data as tables in normal form, we also come to the reflection that our “objects” are just a set of tables and that all possible objects for our system are the set of permutations of all tables.

By using this approach, the implicit state is removed from the storage and is rather a result of a given state of one of our sets. Instead of having an “is delivered”-boolean on a given package, we can check the timeline of locations for the package and see if the last entry is its intended destination. Or if we were making a video game, to check if a given character is dead, instead of having an “is dead”-boolean, rather check if the character’s health points are zero or lower. Now, the implicit states of our system are shown through our procedures that check for these states. One could think of these procedures in the same way we think about whether a certain temperature is “hot” or “cold”, or if a certain speed is “fast”. There is nothing inherent in 200 km/h that makes it fast, it is rather something we determine, given the state and circumstances. In fact, rule builders or rule engines are quite common in e-commerce to calculate offers, taxes, tariffs and so forth.

When we consider all the possible sets and all the possible states of our sets, it suddenly makes a lot more sense to invest in this rule-based approach, rather than keeping track of hidden state on objects or hard-coding methods that constrain us.

We might be tempted to solve some of these rule implementations through interfaces, but instead, we should embrace the futureproofing and backwards compatibility that working with primitives gives us, at the expense of readability and understandability. By avoiding interfaces, we also avoid hierarchies, which, much like in a database, helps us to join any tables together, thus not constraining our “set of all sets” of tables.

In fact, not only does it allow us to freely move data around and to make different parts message each other, but it also avoids the virtual calls that come with interfaces, as well as making our data unordered and thus easier to parallelise, something that is paramount for large data sets.

This is why we also don’t have any global state in our system, everything must fit into a table, for the transformations of our data to be unordered in this way. In fact, we could implement a transactional style of transforms, for added robustness, such as with money transactions. This would be trivial given our DOD system, but a more difficult task in an OOP system, given that different instances of objects must message each other, and sometimes not all of them have access to each other, due to hierarchies.

When we enforce procedures with no side effects as well, we can begin to turn our data into streams, and suddenly take advantage of SIMD and GPU-acceleration such as with compute shaders. If we notice any part of our system slowing down, we can turn it into a stream and make use of the actual hardware, since we haven’t abstracted it and knowledge of its capabilities away.

Conclusion

OOP has been a very successful paradigm since computers became so fast, that it is often more important to help the programmer understand, what is being built, and to avoid regression and bugs when making changes than it is to squeeze the last bit of performance out of the available hardware and make it easy to alter the structure of a program.

While the DOD paradigm doesn’t necessarily have to replace OOP, it is another useful tool for the programmer, and the way it makes one think about data and control flow can be helpful for flattening object hierarchies and making code for the hardware instead of for the programmer.

With the increasing demand for the analysis of large datasets, for instance, in machine learning, it is a paradigm worth considering for some workloads.

Further reading: https://github.com/dbartolini/data-oriented-design and https://www.akkadia.org/drepper/cpumemory.pdf

Author